Chi tiết thông tin

Bài 3: Nhị thức Niu-tơn

105 View

Lý thuyết Nhị thức Niu-tơn

I. TÓM TẮT LÝ THUYẾT

1. Công thức nhị thức Niu-tơn (a + b)ⁿ = C_n⁰aⁿ + C_n¹a^{n - 1}b + … + C_n^ka^{n - k}b^k + … + C_n^n-1ab^n-1 + C_nⁿbⁿ (1) 2. Hệ quả - Với a = b = 1, ta có: 2ⁿ = C_n⁰ + C_n¹ + … + C_nⁿ. - Với a = 1; b = –1, ta có: 0 = C_n⁰ – C_n¹ + … + (–1)^kC_n^k + … + (–1)C_nⁿ. 3. Chú ý: Trong biểu thức ở vế phải của công thức (1): -Số các hạng tử là n + 1; - Các hạng tử có số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước a⁰ = b⁰ = 1); - Các hệ số của mỗi hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

Trả lời câu hỏi trang 55:

Khai triển biểu thức (a + b)⁴ thành tổng các đơn thức. Lời giải: (a + b)⁴ = (a + b)³(a + b) = (a³ + 3a²b + 3ab² + b³ )(a + b) = a⁴ + 3a³b + 3a²b² + ab³ + a³b + 3a²b² + 3ab³ + b⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

Trả lời câu hỏi trang 57:

Dùng tam giác Pa-xcan, chứng tỏ rằng: a) 1 + 2 + 3 + 4 = C²₅; b) 1 + 2 + … + 7 = C²₈. Lời giải: a) Dựa vào tam giác Pa-xcan:C¹₄ = 4; C²₄ = 6 C²₅ = C¹₄ + C²₄ = 4 + 6 = 10 Mà: 1 + 2 + 3 + 4 = 10 ⇒ 1 + 2 + 3 + 4 = C²₅ b)Dựa vào tam giác Pa-xcan:C¹₇ = 7; C²₇ = 21 C²₈ = C¹₇ + C²₇ = 7 + 21 = 28 1 + 2 +⋯+ 7 = ((1 + 7).7)/2 = 28 ⇒ 1 + 2 +⋯+ 7 = C²₈

Bài 1 (trang 57 SGK Đại số 11):

Viết khai triển theo công thức nhị thức Niu – tơn:

Lời giải:

Kiến thức áp dụng

+ Khai triển nhị thức Niu-tơn:

Bài 2 (trang 58 SGK Đại số 11):

Tìm hệ số của x³ trong khai triển của biểu thức :

Lời giải: + Số hạng tổng quát của khai triển

là:

+ x³ ứng với 6 – 3k = 3 ⇔ k = 1. Vậy hệ số của x³ là:

Kiến thức áp dụng

Bài 3 (trang 58 SGK Đại số 11):

Biết hệ số của x² trong khai triển của (1 – 3x)ⁿ là 90. Tìm n. Lời giải: + Số hạng tổng quát của khai triển (1 – 3x)ⁿ là: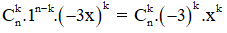 Giải bài tập Đại số 11 | Để học tốt Toán 11

+ Số hạng chứa x² ứng với k = 2. Hệ số của x² là 90 nên ta có:

Vậy n = 5.

Bài 4 (trang 58 SGK Đại số 11):

Tìm số hạng không chứa x trong khai triển của

Lời giải: + Số hạng tổng quát trong khai triển

là:

+ Số hạng không chứa x tương ứng với 24 – 4k = 0 ⇔ k = 6. Vậy số hạng không chứa x trong khai triển đã cho là:

Kiến thức áp dụng

Với các bài toán liên quan đến hệ số của x^m trong khai triển một biểu thức ta thường làm như sau: + Tìm số hạng tổng quát trong khai triển. + Tìm k tương ứng với x^m + Tìm hệ số của x^m tương ứng với k vừa tìm được.