Bài 3: Hàm số liên tục
116 View


Lý thuyết Hàm số liên tục
I. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
Định nghĩa 1 Cho hàm số y = f(x) xác định trên khoảng K và x0 ∈ K. Hàm số y = f(x) được gọi là liên tục tại x0 nếuII. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG
Định nghĩa 2 Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó. Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và Hàm số liên tục trên khoảng (a;b)
Hàm số liên tục trên khoảng (a;b)

III. MỘT SỐ ĐỊNH LÍ CƠ BẢN
Định lí 1 a) Hàm số đa thức liên tục trên toàn bộ tập số thực R. b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng. Định lí 2 Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x0. Khi đó: a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x0; b) Hàm số liên tục tại x0 nếu g(x0) ≠ 0.
Định lí 3
Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0..
Định lí 3 có thể phát biểu theo một dạng khác như sau:
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).
liên tục tại x0 nếu g(x0) ≠ 0.
Định lí 3
Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0..
Định lí 3 có thể phát biểu theo một dạng khác như sau:
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).
Trả lời câu hỏi trang 135:
Cho hai hàm số f(x) = x2 và có đồ thị như hình 55
đồ thị như hình 55
 a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1.
Lời giải:
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1.
Lời giải:
 b)
+ Đồ thị của hàm số y = f(x) là đường liền nét tại điểm có hoành độ x= 1.
+ Đồ thị hàm số y = g(x) là đường không liền nét tại điểm có hoành độ x= 1.
b)
+ Đồ thị của hàm số y = f(x) là đường liền nét tại điểm có hoành độ x= 1.
+ Đồ thị hàm số y = g(x) là đường không liền nét tại điểm có hoành độ x= 1.
Trả lời câu hỏi trang 138:
Trong biểu thức xác định h(x) cho ở Ví dụ 2, cần thay số 5 bởi số nào để được một hàm số mới liên tục trên tập số thực R ? Lời giải: Cần thay số 5 bởi số 2 để được một hàm số mới liên tục trên tập số thực R Trả lời câu hỏi trang 138: Giả sử hàm số y = f(x) liên tục trên đoạn [a; b] với f(a) và f(b) trái dấu nhau. Hỏi đồ thị của hàm số có cắt trục hoành tại điểm thuộc khoảng (a; b) không? ⦁ Bạn Hưng trả lời rằng: “Đồ thị của hàm số y = f(x) phải cắt trục hoành Ox tại một điểm duy nhất nằm trong khoảng (a; b)”. ⦁ Bạn Lan khẳng định: “Đồ thị của hàm số y = f(x) phải cắt trục hoành Ox ít nhất tại một điểm nằm khoảng (a; b)”. ⦁ Bạn Tuấn thì cho rằng: “Đồ thị của hàm số y = f(x) có thể không cắt trục hoành trong khoảng (a; b), chẳng hạn như đường parabol ở hình (h.58). Câu trả lời của bạn nào đúng, vì sao? Lời giải:
- Bạn Lan nói đúng vì f(a) và f(b) trái dấu nên tồn tại ít nhất 1 giá trị x sao cho f(x) = 0, do đó đồ thị hàm số y = f(x) cắt trục hoành tại ít nhất 1 điểm
- Bạn Hưng sai vì có thể có 2 giá trị x sao cho f(x) = 0
- Đường parabol trên hình 58 là đồ thị hàm số y2 = x ⇒ đồ thị hàm số
y = f(x) sẽ là 1 nửa nằm trên hoặc 1 nửa nằm dưới trục hoành
Khi đó f(a) và f(b) cùng dấu, mâu thuẫn với điều kiện f(a) và f(b) trái dấu
Ví dụ của Tuấn sai
Lời giải:
- Bạn Lan nói đúng vì f(a) và f(b) trái dấu nên tồn tại ít nhất 1 giá trị x sao cho f(x) = 0, do đó đồ thị hàm số y = f(x) cắt trục hoành tại ít nhất 1 điểm
- Bạn Hưng sai vì có thể có 2 giá trị x sao cho f(x) = 0
- Đường parabol trên hình 58 là đồ thị hàm số y2 = x ⇒ đồ thị hàm số
y = f(x) sẽ là 1 nửa nằm trên hoặc 1 nửa nằm dưới trục hoành
Khi đó f(a) và f(b) cùng dấu, mâu thuẫn với điều kiện f(a) và f(b) trái dấu
Ví dụ của Tuấn sai
Trả lời câu hỏi trang 139:
Hãy tìm hai số a và b thỏa mãn 1 < a < b < 2, sao cho phương trình trong Ví dụ 3 ở trên có ít nhất một nghiệm thuộc khoảng (a; b). Lời giải: Ta có: y = f(x) là hàm số đa thức liên tục trên R.
Do đó f(x)liên tục trên
y = f(x) là hàm số đa thức liên tục trên R.
Do đó f(x)liên tục trên  Từ đó suy ra,
Từ đó suy ra,
Bài 1 (trang 140 SGK Đại số 11):
Dùng định nghĩa xét tính liên tục của hàm số f(x)=x3+2x-1 tại x0=3. Lời giải: Kiến thức áp dụng
Kiến thức áp dụng
+ Hàm số f(x) liên tục tại x0 nếu 
phương trình f(x) = 0 có ít nhất một nghiệm xo ∈ (0;2)
Bài 1 (trang 140 SGK Đại số 11):
Dùng định nghĩa xét tính liên tục của hàm số f(x)=x3+2x-1 tại x0=3. Lời giải: Kiến thức áp dụng
Kiến thức áp dụng
+ Hàm số f(x) liên tục tại x0 nếu 
 b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x0=2.
Lời giải:
a) Ta có: g(2) = 5.
b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x0=2.
Lời giải:
a) Ta có: g(2) = 5.
 ⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
 Vậy để hàm số liên tục tại x = 2 thì cần thay 5 bằng 12.
Kiến thức áp dụng
Vậy để hàm số liên tục tại x = 2 thì cần thay 5 bằng 12.
Kiến thức áp dụng
Bài 2 (trang 141 SGK Đại số 11):
a) Xét tính liên tục của hàm số y = g(x) tại x0 = 2, biết : b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x0=2.
Lời giải:
a) Ta có: g(2) = 5.
b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x0=2.
Lời giải:
a) Ta có: g(2) = 5.
 ⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
+ Hàm số f(x) liên tục tại x0 nếu 
 a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Lời giải:
a) Đồ thị hàm số (hình bên).
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Lời giải:
a) Đồ thị hàm số (hình bên).
 Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
 ⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
Kiến thức áp dụng
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
Kiến thức áp dụng
 và g(x) = tan(x) + sin(x)
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm liên tục.
Lời giải:
và g(x) = tan(x) + sin(x)
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm liên tục.
Lời giải:

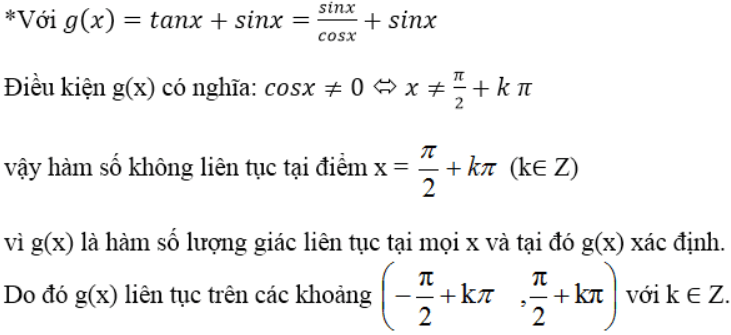 Kiến thức áp dụng
Kiến thức áp dụng
Bài 3 (trang 141 SGK Đại số 11):
Cho hàm số a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Lời giải:
a) Đồ thị hàm số (hình bên).
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Lời giải:
a) Đồ thị hàm số (hình bên).
 Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
 ⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
Kiến thức áp dụng
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
Kiến thức áp dụng
+ Hàm số f(x) liên tục tại x0 nếu 


Bài 4 (trang 141 SGK Đại số 11):
Cho các hàm số và g(x) = tan(x) + sin(x)
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm liên tục.
Lời giải:
và g(x) = tan(x) + sin(x)
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm liên tục.
Lời giải:

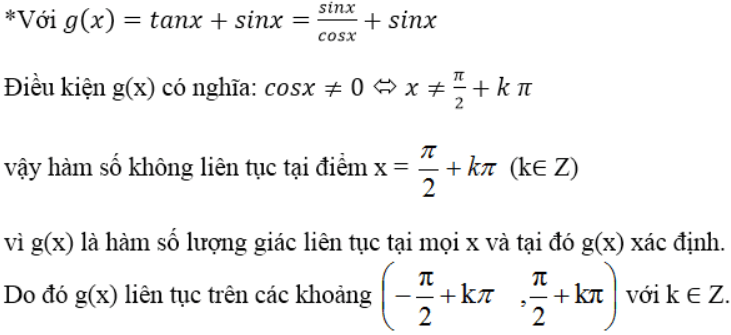 Kiến thức áp dụng
Kiến thức áp dụng
+ Hàm phân thức hữu tỉ và các hàm số lượng giác liên tục trên từng khoảng của tập xác định của chúng.
Bài 5 (trang 141 SGK Đại số 11):
Ý kiến sau đúng hay sai? "Nếu hàm số y = f(x) liên tục tại điểm x0 và hàm số y = g(x) không liên tục tại x0, thì y = f(x) + g(x) là một hàm số không liên tục tại x0". Lời giải: Ý kiến trên đúng. Vì giả sử ngược lại hàm số y = h(x) = f(x) + g(x) là hàm số liên tục tại x0. Khi đó, hàm số g(x) = h(x) – f(x) là hiệu của hai hàm số liên tục tại x0 nên hàm số g(x) là hàm số liên tục x0 ( định lí về hàm số liên tục) => Mâu thuẫn với giả thiết là hàm số g(x) không liên tục tại x0. Kiến thức áp dụng
Hai hàm số f(x) và h(x) liên tục tại x0 thì các hàm số f(x) ± h(x) ; f(x).h(x) cũng liên tục tại x0.
Bài 6 (trang 141 SGK Đại số 11):
Chứng minh rằng phương trình: a. 2x3 – 6x + 1 = 0 có ít nhất hai nghiệm. b. cos x = x có nghiệm Lời giải: a. Đặt f(x) = 2x3 – 6x + 1 TXĐ: D = R f(x) là hàm đa thức nên liên tục trên R. Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = - 3 < 0 f(0) = 1 > 0 f(1) = 2.13 – 6.1 + 1 = -3 < 0. ⇒ f(-2).f(0) < 0 và f(0).f(1) < 0 ⇒ f(x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0) và ít nhất một nghiệm thuộc (0 ; 1) ⇒ phương trình f(x) = 0 có ít nhất hai nghiệm. b. Xét hàm số g(x) = x – cos x liên tục trên R. do đó liên tục trên đoạn [-π; π] ta có: g(-π) = -π – cos (-π) = -π + 1 < 0 g(π) = π – cos π = π – (-1) = π + 1 > 0 ⇒ g(-π). g(π) < 0 ⇒ phương trình x – cos x = 0 có nghiệm trong (-π; π) tức là cos x = x có nghiệm. Kiến thức áp dụng
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0 thì tồn tại ít nhất 1 điểm c ∈ (a; b) sao cho f(c) = 0.
Các bài viết liên quan
Các bài viết được xem nhiều nhất
5 tác phẩm trọng tâm ôn thi THPT Quốc gia 2024 môn Ngữ Văn khả năng...
26170 View
Đáp án CHÍNH THỨC đề thi tốt nghiệp THPT 2023 từ Bộ GD&ĐT (Tất cả...
1123 View
Đề thi tốt nghiệp THPT Quốc gia năm 2023 môn Địa lí và gợi ý giải...
1048 View
Đề thi tốt nghiệp THPT Quốc gia năm 2023 môn Giáo dục công dân và gợi...
1035 View
Link tra cứu điểm thi THPT Quốc gia 2023 toàn quốc 63 tỉnh thành. Cách xem...
962 View
Theo dõi Captoc trên




